12:14 07-03-2004 Творческая задача
Задача Мелзака
У какого выпуклого многогранника заданного объема периметр наименьший?
Примеры: у куба объемом 1 периметр 12. Но это не куб У равностороннего тетраэдра периметр 12.24. У равностороннего пентагранника, aka фигуры Фелана-Вейре, aka dice d12, все стороны-пятиугольники, - между 14 и 16, сегодня часа три считал.
У равностороннего тетраэдра периметр 12.24. У равностороннего пентагранника, aka фигуры Фелана-Вейре, aka dice d12, все стороны-пятиугольники, - между 14 и 16, сегодня часа три считал.
<_____лирическое отступление раз__>
Фигура Фелана-Вейре была получена, как нетрудно догадаться, Phelan'ом и Weaire в качестве противоречия столетней гипотезе Кельвина о разделение трехмерного пространства на куски так, чтобы суммарная площадь поверхности одной ячейки была минимальной. Известный некоторым читателям дневника Михаил Гиршфельд года полтора назад придумал фигуру Фелана-Вейре где-то за полчаса, когда я ему задал задачу про лучшую упаковку шариков в трехмерном пространстве.
<____лирическое отступление два___>
Задача про упаковку шариков впервые возникла на курсах для поступления в ВГУ, на которых кроме меня был еще Velmar. Только тогда она была в двухмерном пространстве, шарики упаковывались в гексы. Потом я ее обобщил на трехмерное пространство и сам дошел примерно до того же, что и Лорд Кельвин.
Поздравьте Михаила Гиршфельда
Первая картинка - тетракайдекахидра (я это слово запомню!) Кельвина
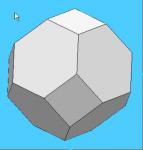
Вторая картинка - фигура Фелана-Вейре-(Гиршфельда )
)
А теперь все решают задачу Мелзака!
У какого выпуклого многогранника заданного объема периметр наименьший?
Примеры: у куба объемом 1 периметр 12. Но это не куб
<_____лирическое отступление раз__>
Фигура Фелана-Вейре была получена, как нетрудно догадаться, Phelan'ом и Weaire в качестве противоречия столетней гипотезе Кельвина о разделение трехмерного пространства на куски так, чтобы суммарная площадь поверхности одной ячейки была минимальной. Известный некоторым читателям дневника Михаил Гиршфельд года полтора назад придумал фигуру Фелана-Вейре где-то за полчаса, когда я ему задал задачу про лучшую упаковку шариков в трехмерном пространстве.
<____лирическое отступление два___>
Задача про упаковку шариков впервые возникла на курсах для поступления в ВГУ, на которых кроме меня был еще Velmar. Только тогда она была в двухмерном пространстве, шарики упаковывались в гексы. Потом я ее обобщил на трехмерное пространство и сам дошел примерно до того же, что и Лорд Кельвин.
Поздравьте Михаила Гиршфельда
Первая картинка - тетракайдекахидра (я это слово запомню!) Кельвина
Вторая картинка - фигура Фелана-Вейре-(Гиршфельда
А теперь все решают задачу Мелзака!
Комментарии:
13:18 07-03-2004
А у прямой треугольной равонореберной призмы объемом 1 периметр 11,8962....
отредактировано: 07-03-2004 13:36 - vakito
13:41 07-03-2004
vakito
Ага
Но минимум ли это?
Ага
Но минимум ли это?
13:51 07-03-2004
Xirax
а вообще какой тут может существовать принцип доказательства минимума?
может потыкаться в версию, что с увеличением числа ребер периметр неуменьшается?
а вообще какой тут может существовать принцип доказательства минимума?
может потыкаться в версию, что с увеличением числа ребер периметр неуменьшается?
14:06 07-03-2004
vakito
Нету никакого принципа доказательства.
Надо придумать фигуру, у которой периметр будет меньше, чем у треугольной призмы.
Пока что удалось доказать, что искомая фигура, если она вообще существует, должна быть не призмой -- т.к. периметр равнореберной призмы с правильным n-угольником в основании растет с увеличением n.
Нету никакого принципа доказательства.
Надо придумать фигуру, у которой периметр будет меньше, чем у треугольной призмы.
Пока что удалось доказать, что искомая фигура, если она вообще существует, должна быть не призмой -- т.к. периметр равнореберной призмы с правильным n-угольником в основании растет с увеличением n.
23:56 07-03-2004
Kaineg
То для тотально равнобокой призмы... А если у нее высота меньше стороны основания? Надо дифференцировать для общего случая...
То для тотально равнобокой призмы... А если у нее высота меньше стороны основания? Надо дифференцировать для общего случая...
00:02 08-03-2004
Кстати, для пентагональной призмы я посчитал неправильно, получилось 12.52, что не так плохо
00:07 08-03-2004
Мда, общее дифференцирование только что показало, что наилучший результат как раз когда высота равна стороне 
03:05 08-03-2004
Исключил пирамиды.
05:25 08-03-2004